Special Relativity with Geometric Algebra - Introduction
What is Special Relativity?
Special Relativity published by Albert Einstein in 1905 makes clearer the relation between time and space in physics. It does this by unifying them and introducing two postulates:
Postulate 1
The laws of physics are the same in all inertial reference frames.An inertial reference frame is the frame of an unaccelerated observer, ie. one moving with constant velocity. The postulate says that for such frames, we can write down formulas which will be true for all observers even if their velocity is different. The more general case with accelerated reference frames is treated in Einstein's General Relativity.
Postulate 2
The speed of light (in vacuum) is the same for all observers.Meaning, no matter the motion of the observer, light will always move at the speed of light.
These postulates might seem trivial for now (everybody knows that light always moves at the speed of light right?), but we will see that that they have huge consequences. If you are already familiar with Special Relativity, you will probably also see that the treatment with Geometric Algebra simplifies a lot of things.
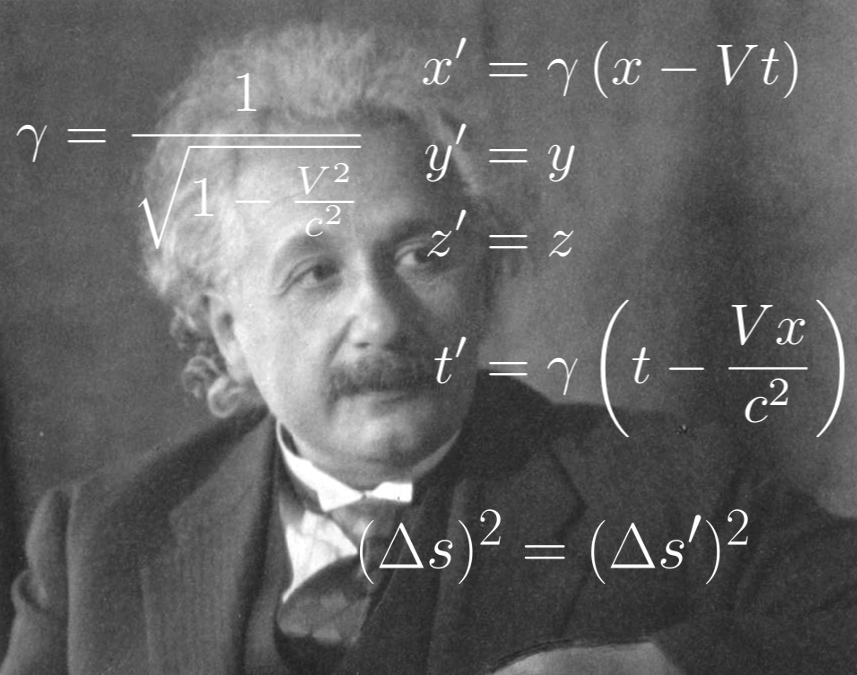
Why Special Relativity?
Without Special Relativity, we will see that addition of velocities breaks down at speeds close to the speed of light. We will also notice many interesting phenomena such as electric fields being seen as magnetic fields by observers moving at high speeds relative to them, shedding light on the duality between the two. Furthermore it provides a pathway for understanding General Relativity which is the basis for our best models of gravity.
References
Geometric Algebra
This series assumes you already know the basics of Geometric Algebra and rotors. There are a couple of articles about that on this website but there are also fantastic introductions on YouTube:
- A Swift Introduction to Geometric Algebra by Sudgy who is also working on a complete Geometric Algebra series
- Geometric Algebra playlist by Mathoma
- Let's remove Quaternions from every 3D Engine: Intro to Rotors from Geometric Algebra by Marc ten Bosch (with accompanying article)
- Various videos on the Bivector channel
There are also various books that cater to different audiences, to name a few:
- Geometric Algebra for Computer Science by Leo Dorst
- Geometric Algebra for Physicists by Anthony Lasenby and Chris Doran: Mostly assumes knowledge of physics in the ordinary formalism and introduces them with GA, covers a lot of topics and even General Relativity. I used this book a lot to learn about Special Relativity (and other topics).
- Geometric Algebra for Electrical Engineers by Peeter Joot: What I like about this one is that it does not contain much "noise", just straight usefulness
- Linear and Geometric Algebra by Alan Macdonald
The website bivector.net also contains links to more resources as well as our community discord. Feel free to join and ask questions!
Special Relativity
There are many excellent videos on YouTube about Special Relativity, for example The Science Asylum's video great. Leonard Susskind has a recorded lecture series about Special Relativity here. His lectures are always amazing. For books I can only recommend "Geometric Algebra for Physicists" mentioned above. I haven't looked into any specific non-GA books about Special Relativity.