Geometric Algebra

Geometric Algebra > Special Relativity with Geometric Algebra - Geometric Algebra Review

Special Relativity with Geometric Algebra - Geometric Algebra Review

Ordinary 3D Geometric Algebra

Let's review a couple of properties of ordinary 3D Geometric Algebra. If you are not yet familiar with it there are a few excellent videos on YouTube as well as a couple of books going into GA in more detail. A few were mentioned in the previous section.

_{Figure 1 - Blue: Orthonormal basis vectors. Red: Position vectors $a, b$ . Yellow: difference vector $v$ from $a$ to $b$ .}

We have three orthonormal basis vectors

e_{x}, e_{y}, e_{z}

. Written using the Kronecker delta we have

e_{i} \cdot e_{j} = δ_{j}^{i}

, which says that the inner product of two same basis vectors is

1

, and the inner product of two different basis vectors is

0

. For example we have

e_{x} \cdot e_{x} = 1

and

e_{x} \cdot e_{y} = 0

The position vectors

a

and

b

from figure 1 can be written terms of the basis vectors as follows

\begin{matrix} (1) & \begin{aligned} a & = a_{x} e_{x} + a_{y} e_{y} \\ b & = b_{x} e_{x} + b_{y} e_{y} \end{aligned} \end{matrix}

We can form the difference vector

v

from

a

b

by subtracting

a

from

b

to get

\begin{matrix} (2) & v = b - a = (b_{x} - a_{x}) e_{x} + (b_{y} - a_{y}) e_{y} = Δ x e_{x} + Δ y e_{y} \end{matrix}

To get the length squared

| | v | |^{2}

we have to square

v

, which yields the same result as the Pythagorean theorem

\begin{matrix} (3) & | | v | |^{2} = v^{2} = (Δ x e_{x} + Δ y e_{y})^{2} = Δ x^{2} + Δ y^{2} \end{matrix}

Active and Passive Transformations

You might not have heard the terms active and passive transformations before, but it is often a useful distinction to make. We will review these two types of transformations now too.

Active Transformations

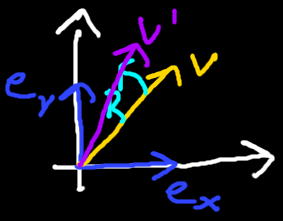
_{Figure 2 - Blue: Orthonormal basis vectors. Yellow: Original vector. Teal: Active transformation rotor. Purple: Original vector transformed using rotor.}

Active transformations change objects. The active transformations we are interested in here are those with rotors. In ordinary 3D GA we have three basis blades

e_{x y}, e_{y z}, e_{x z}

which can be used to rotate in the planes denoted by their subscripts. For example, as in figure 2, a rotor that rotates by an angle

φ

in the XY plane is formed like this

\begin{matrix} (4) & R_{x y} = e^{- \frac{φ}{2} e_{x y}} = \cos (- \frac{φ}{2}) + \sin (- \frac{φ}{2}) e_{x y} \end{matrix}

The rotor is then applied to an object, such as our vector

v

, with a two-sided product often called the sandwich product

\begin{matrix} (5) & v^{'} = R_{x y} v {\tilde{R}}_{x y} \end{matrix}

The resulting vector

v^{'}

will in general be different from

v

, so this is an active transformation as the object did actually change.

Rotating a vector does not change its length (verify this as an excercise if you wish by squaring the rotated vector), so applying rotors preserves distances.

\begin{matrix} (6) & | | v^{'} | |^{2} = | | R_{x y} v {\tilde{R}}_{x y} | |^{2} = v_{x}^{' 2} + v_{y}^{' 2} = v_{x}^{2} + v_{y}^{2} = | | v | |^{2} \end{matrix}

Passive Transformations

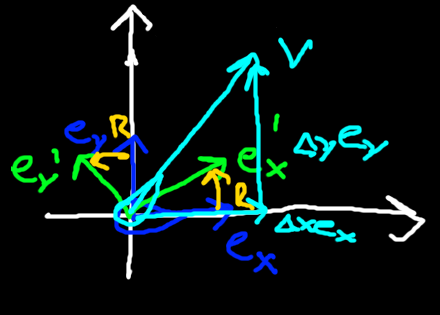
_{Figure 3 - Coordinate system using original orthonormal basis vectors. Blue: Original orthonormal basis vectors. Yellow: Passive transformation rotor. Green: Original orthonormal basis vectors transformed with rotor. Teal: Vector.}

Passive transformations act on the coordinate basis vectors. They do not actually change the objects, only the perspective on them. They are also called change of basis. We are interested in passive transformations performed by rotors.

Let's say our first set of basis vectors

e_{x}, e_{y}

belonged to one person. We have another person with basis vectors

e_{x}^{'}, e_{y}^{'}

who is looking in another direction from the first person such as in figure 3. The rotation between the first and second set of basis vectors can be performed by a rotor

R

\begin{matrix} (7) & \begin{aligned} e_{x}^{'} & = R e_{x} \tilde{R} \\ e_{y}^{'} & = R e_{y} \tilde{R} \end{aligned} \end{matrix}

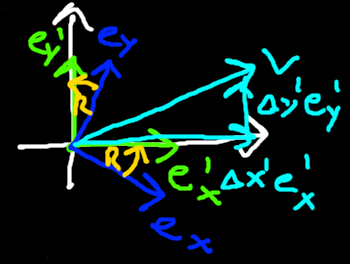
_{Figure 4 - Coordinate system using transformed orthonormal basis vectors. Blue: Original orthonormal basis vectors. Yellow: Passive transformation rotor. Green: Original orthonormal basis vectors transformed with rotor. Teal: Vector.}

We can now see how the second person views the world by drawing the coordinate system using their basis vectors. The vector

v

appears to rotate in the opposite direction. It is very important to note though that the vector does not actually change. It is merely viwed in a different basis but it is fundamentally the same vector. The vector

v

expressed in the old and the new basis is

\begin{matrix} (8) & v = v_{x} e_{x} + v_{y} e_{y} = v_{x}^{'} e_{x}^{'} + v_{y}^{'} e_{y}^{'} \end{matrix}

As the vector did not actually change, its length when expressed in the new basis is still be the same as before too.

\begin{matrix} (9) & | | v | |^{2} = (v_{x}^{'} e_{x}^{'} + v_{y}^{'} e_{y}^{'})^{2} = v_{x}^{' 2} + v_{y}^{' 2} = v_{x}^{2} + v_{y}^{2} \end{matrix}

Another important property of passive transformations with rotors is that they keep the basis vectors orthonormal.

Important note: In this series we will only be dealing with orthonormal bases to simplify things. This excludes coordinate system such as spherical coordinates. In order to deal with more general bases a concept called reciprocal frames is required. Overall this is not a big change to make however, and it would be easy to adjust all our upcoming results to use them.

Conclusion

We shortly reviewed position and difference vectors. We looked at active transformations which change objects, in particular active transformations with rotors which perserve lengths. We also looked at passive transformations which only affect coordinate basis vectors but do not actually affect any objects. For these we also noticed that the length of vectors can obtained using the coefficients of the vector in the transformed basis. Furthermore passive transformations with rotors keep orthonormal bases orthonormal.

Formulas

Orthonormal basis for ordinary GA: $e_{i} \cdot e_{j} = δ_{j}^{i}$
Vector expressed in basis: $v = v_{x} e_{x} + v_{y} e_{y}$
Vector length squared: $| | v | |^{2} = v^{2} = v_{x}^{2} + v_{y}^{2}$
Active transformation with rotor: $v^{'} = R v \tilde{R}, | | v^{'} | |^{2} = | | v | |^{2}$
Passive transformation with rotor: $e_{i}^{'} = R e_{i} \tilde{R}, e_{i} \cdot e_{j} = δ_{j}^{i} ⟺ e_{i}^{'} \cdot e_{j}^{'} = δ_{j}^{i}$

Up next

Next we will look at how we can describe Spacetime with Geometric Algebra motivated by a thought experiment.