Special Relativity with Geometric Algebra - Spacetime Rotors
Velocity addition close to the speed of light
To motivate spacetime rotors, we need more trains (these are very popular in relativity apparently).
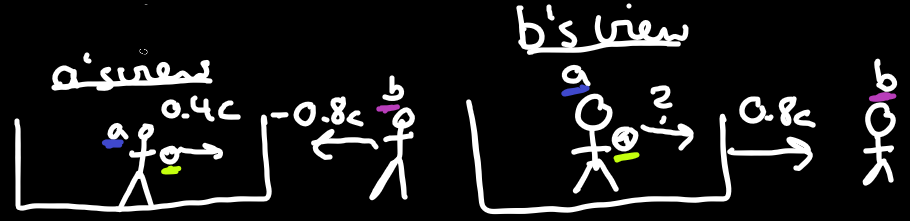
Consider Alice is now on a train. On the train, she is throwing a ball with speed
If we just add up the speed of the train as seen by Bob and the speed of the ball as seen by Alice we get
- From the paths section we know that the angle of paths is related to their speed
- We also know that resting observers have path velocities proportional to
- Claim: We can use our new rotors to rotate between path velocities to find the correct velocity from Bob's perspective
Okay this might sound far-fetched first. Rotate between spacetime velocities? Let's look at this sketch.
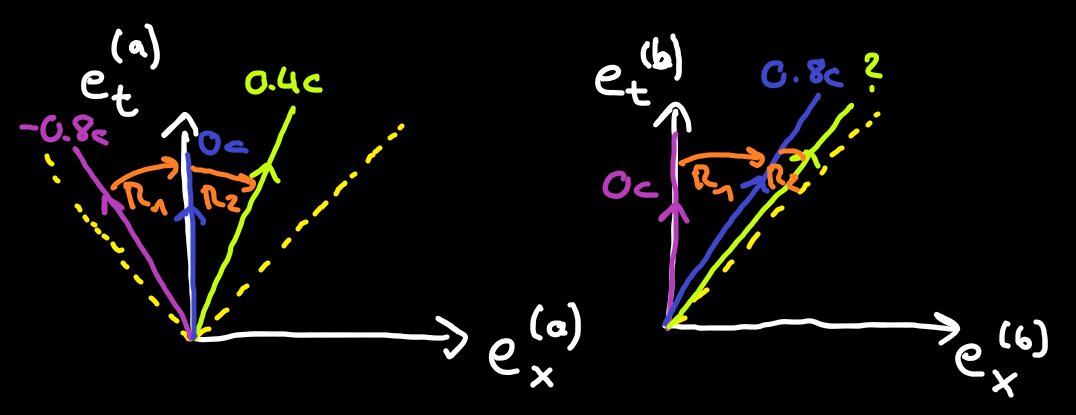
Alice's view (left)
Alice (blue) is at rest so her path velocity vector points in her
The rotations between these vectors are all active transformations because the three velocity vectors are actually different from each other and it is not just Alice changing her perspective on a single unchanging vector.
Bob's view (right)
Bob's velocity vector (purple) is at rest, ie. points in his
Velocity Rotors
Now the key observation: the rotors in the left and the right diagram are identical. The values in them are the same (unlike for the vectors!). So if we know them in one diagram we can use them in the other. We know
So that's the idea. How to actually do this and how the angle relates to the speed comes in the next section.
Rotors in the Spacetime Algebra
To continue, we need to look at what the rotors in the Spacetime Algebra actually do. We will only need the rotors for bivectors squaring to
Can we expand this further? Usually we get something involving sine and cosine for performing ordinary rotations, but that is because the bivector in the exponential squared to
What does this rotor do? It's not ordinary rotation, it is hyperbolic rotation! What is hyperbolic rotation? I promised you earlier we could use these rotors to rotate velocity vectors and use them for velocity addition. Let's apply them to the rest velocity vector
The steps between the left-hand side and right-hand side are left as an excercise. This will require some identities involving the hyperbolic sine and cosine functions, or you can just throw them into Wolfram Alpha to see what the parts simplify to.
We can see the result is some mix of
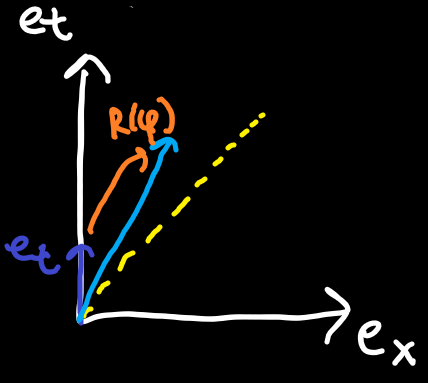
To get some more intuition let's look at the slope of the result. The
So the slope is equal to one over the hyperbolic tangent

The second part we need for plotting what the result looks like is the length of the resulting vector. The length in our graph is the euclidean length. This is of course not the length / distance we use in the algebra, but in our drawings, if the
Now we take a deeper look at the slope result we got earlier for different rotor angles
If
Relation between velocity and angle
Given what we learnt, we can try to figure out the relationship between the angle
We will use this relation in the next section to finally solve our velocity addition problem.
Velocity addition close to the speed of light: revisited

And we're back. This time equipped with the power of rotors that can rotate velocities and the relation between angles and velocities! We want to figure out the velocity of the ball from Bob's perspective (which we don't know yet). For that we look at Bob's frame where he is at rest and apply the two rotors (which we do know). Let me show you one more thing (that you probably already knew!) about rotors before we tackle the problem.
When we compose two rotors in the same plane we get (no matter what the bivector squares to)
When composing two rotations the angles just add. This is still the case even with our hyperbolic rotations. It turns out to solve the problems we don't even need to use rotors directly. First we calculate the two angles corresponding to the two velocities we were given. To get the angle from velocity we solve
The ball moves at around
Conclusion
We started by noticing that adding velocities close to the speed of light fails with ordinary addition because the speed of light can be exceeded. We then saw how we can relate velocity vectors using rotors with bivectors that square to
Formulas
- Relation between angle and velocity:
- Addition of angles:
- Addition of velocities:
Up next
Next we will look at how we can take measurements in Spacetime.